5. Algorithms for Competitive Programming
5.1. Number Theory/ Math:- Prime Numbers
- Go till Sqrt(n)
void isPrime(int n){
if (n==1) return false;
for(int i=2; i*i<=n ; i++){ // optimization - go till sqrt(n)
if(n%i==0){
return false;
}
}
return true;
}
If a prime number is >=5, then it's either of the form 6n-1 or 6n+1. But not vice-versa (25, 49 are not prime)
Sieve of Eratosthenes (Find all prime numbers from 0 to N in NlogN)
void generatePrimeSieve(int n){
const int arrSize = n+1;
bool isPrimeSieve[arrSize]; // 0 to n values
fill(isPrimeSieve, isPrimeSieve+arrSize, true);
isPrimeSieve[0] = false; // 0 is not a prime number
isPrimeSieve[1] = false; // 1 is not a prime number
for(int i=2; i*i<=n; i++){
if(isPrimeSieve[i]){
// go from i*i to n with step of i.
for(int j = i*i ; j<=n; j+=i){
// going over i^2, i^2+i, i^2+2i, i^2+3i ... n
isPrimeSieve[j] = false;
}
}
}
// printing all prime numbers
for(int i=2; i<=n; i++){
if(isPrimeSieve[i]) {
cout<<i <<",";
}
}
cout<<endl;
}Segmented Sieve (Find all prime numbers in the range [L, U], where L, U < 10^12 and L-U <=10^6)
- The problem with Normal Sieve is that it needs to form an array of Size N(10^12 here). Now this limits the range of N as we cannot create an array of Size N as big as 10^12 in memory. Hence we use a Segmented Sieve.
- Step1: Calculate all primes till sqrt(N)and mark a multiple of these primes in the segmented Sieve array as false.
- Step2: Just map the array index to the range. 0th index to L, 1st to L+1, and so on.
- Hence need to create an array of size U-L only, which is 10^6, which we can create in memory.
Prime factorization of number N
Trial Division : O(sqrt(n))
// Fact:- Smallest divisor of a Number N, is always a prime Number, and that is always <= sqrt(N)
void factorize(int n){
for(int i = 2; i * i <= n; i++){
while(n % i == 0) {
cout << i << endl;
n = n / i;
}
}
// Fact:- n = p^a * q^b* r^c * s^d => only one p,q,r,s can be greater than sqrt(N), rest of them will always be <= sqrt(N)
if(n != 1) cout << n << endl;
}// Fact:- Smallest divisor of a Number N, is always a prime Number, and that is always <= sqrt(N)
vector<pair<int, int> > pfs;
for (int i = 2; i*i <= n; i++) { // O(sqrt(n))
if(n % i == 0) {
int cnt = 0;
while(n % i == 0){ // log(n)
n /= i;
cnt++;
}
pfs.push_back({i,cnt});
}
}
// Fact:- n = p^a * q^b* r^c * s^d => only one p,q,r,s can be greater than sqrt(N), rest of them will always be <= sqrt(N)
if(n != 1) pfs.push_back({n,1});optimization would be to iterate over primes < n vector and calculating.
- use sieve of Eratosthenes to get primes list up till n. O(Nloglogn):
precomputation - loop over primes vector.
vector<int> primes = sieve(); // O(nloglogn)
vector<pair<int, int> > pfs;
// per query:- O(#primes < sqrt(N))
// Not a major optimization!
for (int i = 0; primes[i]*primes[i] <= n; i++) {
if(n%i==0){
int cnt = 0;
while(n%i==0){
n/=i;
cnt++;
}
pfs.push_back({i,cnt});
}
}
// Fact:- n = p^a * q^b* r^c * s^d => only one p,q,r,s can be greater than sqrt(N), rest of them will always be <= sqrt(N)
if(n!=1){
pfs.push_back({n,1});
}- use sieve of Eratosthenes to get primes list up till n. O(Nloglogn):
Other way is to modify the sieve of erathosthenes only.
Store the smallest divisor of a number in sieve array. (Pre-computation:
vector<int> spfs) -> spf: smallest prime factor of a number.Why? To do the prime factorization like we did in school!.
int N = 10000;
vector<int> sieve () {
vector<int> spfs(N);
for(int i = 2; i < N; i++) spfs[i] = i;
for(int i = 2; i < N; i++) {
if(spfs[i] == i) { // i is prime
for(int j = i*i; j < N; j+=i) if(spfs[j] == j) spfs[j] = i;
}
}
return spfs;
}
vector<int> spfs = sieve(); // O(nloglogn)
vector<pair<int, int> > pfs;
// per query:- O(logn)
while(n > 1) { // O(logn)
cout << spfs[n] <<endl;
n /= spfs[n];
}
Conclusion
- If per-query is not an issue, can use sqrt(n) or #primes on sieve method.
- else, precompute in nloglogn & pre-query use log(n)- method spf using sieve.
Divisors of number N - O(sqrt(N))
- iterate from 1 to sqrt(N), and report i and n/i, if n%i == 0.
vector<int> divisors;
for(int i = 1; i*i <= n; i++){
if(n % i == 0) divisors.push_back(i);
if(i*i != n) divisors.push_back(n / i);
}
Segmented Sieve
Q:-Find the primes in the range [a,b] where 0 <= a <= b <= 1e12, but (b - a) <= 1e6
- Can't do sieve as can not create array of size 1e12.
- We use segemented Sieve and shift array position.
int n = 1e6 + 1;
int seive[n];
// O((b - a) * loglogb)
void segementedSieve () {
for(int i = 0; i < n; i++) seive[i] = 1;
// O(sqrt(b))
for(int i = 2; i * i <= b; i++) {
int startingPoint = (a / i) * i;
for(int j = startingPoint; j <= b; j += i){
if(j - a >= 0) seive[j - a] = 0;
}
}
for(int i = 0; i < n; i++){
if(seive[i] == 1 and i + a <= b) cout<< i + a << " ";
}
}
Euler Totient Function Φ(x)
- Phi(x) = # of numbers in range [1, x], whose gcd(a, x) = 1; i.e. number is coprime with x.
- Phi(x) = x*(1 - 1/p1)*(1 - 1/p2)*(1 - 1/pn)
int n = 1e6;
int phi[n];
for(int i = 0; i < n; i++) phi[i] = i;
for(int i = 2; i < n; i++) {
if(sieve[i]) { // if i is prime
for(int j = i; j < n; j+=i){
phi[j] -= phi[j]/i;
}
}
};
- Properties of totient function:-
- phi(primeNumber) = primeNumber - 1;
- phi(primeNumber^k) = primeNumber^k(1 - 1/primeNumber);
- phi(ab) = phi(a) phi(b); if gcd(a,b) = 1;
GCD/HCF via Euclid theorem
Euclid algo of multiplication:
BEST: O(log(min(a,b)))Facts:-
- If one is 0, ans is the other one.
- gcd of two numbers doesn't change if we update a larger number with a reminder of two.
int gcd(int a, int b){
if(a == 0 || b == 0) return a ^ b;
return gcd(b, a%b);
}
Euclid algo of subtraction - Time complexity is O(max(a,b)). If a=1 and b=n then it will run n times.
above method is derived from this subtraction only. but since multiple subtraction is equals to modulo. we use above one.
The GCD of two integers may also be worked out by repeatedly replacing the larger of them by the difference of the two.
This simpler version of Euclid's algorithm is less efficient than the usual one described above (using Euclidean division rather than mere subtraction) but it can be convenient in proofs and other theoretical arguments.
Facts:-
- If one is 0, ans is the other one.
- gcd of two numbers doesn't change if we update a larger number with the difference of two.
int gcd(int a, int b){
if(b == 0) return a
if(a == 0) return b
// can be combinded, if(a==0 || b == 0) return a ^b
return gcd(b, abs(a - b));
}
LCM = (a*b)/(gcd(a,b))GCD(A,B) can be represented as product of min(pi^ai, pi^bi) for each prime factor pi.
LCM(A,B) can be represented as product of max(pi^ai, pi^bi) for each prime factor pi.
GCD(A,B,C,D) can be represented as GCD(GCD(GCD(A,B),C),D)
LCM(A,B,C,D) can be represented as LCM(LCM(LCM(A,B),C),D)
GCD(A, A + 1) = 1
Modular Exponentiation. (Finding a^b mod m)
power(a,b,m)
- Naive Approach : power(a,b,m) = (a * power(a,b,m)) % m -> O(b)
- Log(b) Approach and recursive:
- power(a,b,m) = b is Even: (power(a,b/2,m)* power(a,b/2,m)) % m
- = b is Odd: (a power(a,b/2,m) power(a,b/2,m)) % m
- Don't forget to use ab % m = (a % m b % m) % m
- via Binary Decimal system[Log(b) and iterative version of recursive version].
- put b in binary do get logb terms. and multiple (a^2^ith) binary digit in a for loop.
void calpow(int a, int b, int m){
int ans = 1;
while (b) {
int lastBinaryDigit = b&1;
ans = (1LL*ans *(lastBinaryDigit ? a : 1)) %m ; // option 1: 1LL to typecast ans into long long
a = (1LL*a*a) %m; // option2: We could have taken ans and a as long long instead of int.
b = b >>1;
}
return ans;
}
// option 2
void calpow(long long a, long long b, long long m){
long long ans = 1;
while (b) {
long long lastBinaryDigit = b&1;
ans = ans *(lastBinaryDigit ? a : 1) %m ;
a = a*a %m;
b = b >>1;
}
return ans;
}
Modulo Arithmetic Conclusion
int mod_add(int a, int b, int m){
return (a%m + b%m) %m;
}
int mod_sub(int a, int b, int m){
return (a%m + b%m - m) %m;
}
int mod_mul(int a, int b, int m){
return (a%m * b%m) %m;
}
int mod_expo(int a, int b, int m){
if(b == 0) return 1;
int res = mod_expo(a, b / 2, m);
res = mod_mul(res, res, m);
if(b & 1) res = mod_mul(res, a, m);
return res;
}
// works only if m is prime: Fermet's little Theorem
int mod_inv(int a, int m) {
return mod_expo(a, m - 2, m);
}
int mod_div(int a, int b, int m){
return mod_mul(a * mod_inv(b, m), m);
}
Beware
- mod is calculated for integers values.
- 2.5 % m --> is not a valid operation (lhs should be integer.)
- hence (a / b) % m, is calculated for a/b = integer, not a float. Because modulo is the integer partition of space.
- Ex: (n / 2) %modm is not equal to n * mod_inv(2), when n is odd.
Meaning of A congruent to B mod C
[A ≅ B mod C]=> A is equal to B in the modular domain of C.Example
7 ≅ 2 mod 5=>7mod5 ==? 2mod5. Ans is YES.Since AmodC = BmodC = r,
=> A mod C = q1*C + r
=> B mod C = q2*C + r
=> A-B = (q1-q2)C =>
C divides (A-B) completely=>C divides (B-A) completely=> A = B+kC for some k.Distributive Properties
- (a + b) % m = (a % m + b % m ) % m
- (a - b) % m = ((a % m - b % m) % m + m) % m;
- here
(a % m - b % m)part can be -ve. - example -3 mod 2 gives you -1. => add 2 to it and then take mod.
- here
- (a * b) % m = (a % m * b % m ) % m
- (a ^ b) % m = ((a % m)^b) % m; ---------- here
^means power.
- (a ^ b) % m = ((a % m)^b) % m; ---------- here
- (a / b) % m = (a * inverse(b))% m
- (a / b) % m = (a % m * inverse(b) % m ) % m
- (a / b) % m = (a % m * MMI(b, m)) % m
inverse(b)%m = MMI(b, m) is called Modulo Multiplicative Inverse.
VVVIMP. Note😎😎😎:: since answer after modulos can always become -ve, always return ans as
(ans % mod + mod) % mod.😎😎😎
Calculating ncr mod p
ncr is the number of ways of
choosing robjects out ofn distinctelements.Factorial Method is pretty straightfroward,
just use for loop to calculate factorial mod p -> O(n).
Factorial[0] = 1, Factorial[i] = (Factorial[i-1]*i)%p
Note: P should be prime(gcd(a,p)==1) for Inverse to exist. (So we can't use this method if P is not prime.)
calculate MMI of denominators via fermet's result -> O(logP).
total = O(nlogp) = O(nlogp), for each i.
Let we have no. of testcases = 1e5 and for each test case n can go upto 1e5.
- we get TLE.
- but we can do pre-computation/caching Approach: calcute factorial of numbers till N in an array. and then use them in calculation for each test case.(per query -> logn now)
- we can also precompute the MMI of numbers to make everything for a test case O(1). per query O(1) :)
- Time Complexity: O(t*(1 + logp)) < 1e8. No TLE 😁.
void solve(){
int mod = 1e9 + 7;
int n = 1001000;
int fact[n];
int invFactmod[n];
fact[0] = 1;
//O(nlogn)
for(int i = 1; i <= n; i++){
fact[i] = (fact[i - 1] * i) % mod;
invFactmod[i] = powMod(fact[i], mod - 2);
}
int calc(int n, int r){
int num = fact[n];
int invDemo = (1LL * invFactmod[n-r] * invFactmod[r]) % mod;
return num * invDemo;
}
while(q--){
int n,r;
cin >> n >> r;
cout<<calc(n,r)<<endl;
}
}
Multiplication Method
works when
n can be of very big order(10^18)but eitherrorn-ris small(< 10^6).we can cancel many numerator terms as either r or n-r will be of order n.
Here also P must be prime(same reason as above, there will be terms in denominator).
// O(min(r, n-r))
void solve(){
int ncr = 1;
for(int i = 1; i <= min(r, n - r); i++){
ncr = ncr * (n - i + 1) / i;
}
}
Pascal's triangle Method
- ncr = (n-1)c(r-1) + (n-1)c(r) i.e sum of previous rows same column and column-1 elements.
1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1- can maintain a matrix to store these values O(n^2).so use when n<=4000
- can work for any p even if it is not prime, i.e composite.
Some formulas of Binomial Coefficients
nc0 + nc1 + nc2 +.....ncn = 2^n
0nc0 + 1nc1 + 2nc2 +.....ncn = n2^(n-1) // differntiation of above eq.
kck + (k+1)ck + (k+2)ck +.....nck = (n+1)c(k+1) // Hockey Stick Formula
nC0 + (n - 1)C1+ (n - 2)C2+ (n - 3)C3 + ... + (n/2)Cn/2 = Fib(n + 1) // sum of diagonals in pascal trianlge is Fibonocacci number.
#Solutions of x1 + x2 + x3 + ... + xk = n, where each xi > 0
# solutions = (n - 1)C(k - 1)
#Solutions of x1 + x2 + x3 + ... + xk = n, where each xi >= 0 (Bar and stick formula)
# solutions = (n + k - 1)C(n) = (n + k - 1)C(k-1)
#Solutions of x1 + x2 + x3 + ... + xk <= n, where each xi >= 0
- Can be converted to x1 + x2 + x3 + ... + xk + alpha = n, where each xi, alpha >= 0
# solutions = (n + k)C(n) = (n + k)C(k)
Questions:-
Catalan Number
- Cn = 2nCn / (n + 1)
- Recurrence Relation = Cn = Sum(Ci*Cn-i); for all i belongs to [0, n]
Extended Euclidean Algorithm O(log(min(a,b)))
It gives us the solution (x,y) such that
Ax + By = gcd(A,B)holdsx and y will always have integral solutions (Because C = gcd(A,B) which obviously divided by gcd(A,B)).
Solving it
Ax+ By = gcd(A,B) -------- (1)
[as we know gcd(A,B) = gcd(B,A%B)] ---- (2)
gcd(B,A%B) = Bx' + (A%B)y' ----------- [from (1)]
[we Also know that A%B = A - floor(A/B)*B] from Quotient-remainder theorem
gcd(B,A%B) = Bx' + (A - floor(A/B)*B)y'
gcd(B,A%B) = B(x' - y'*floor(A/B)) + Ay'
[from 2]
we get, Ax + By = B(x' - y'*floor(A/B)) + Ay'=> x = y' and
=> y = x' - y'*floor(A/B)
It helps us find the multiplicative Modulo Inverse of a Number.
struct Triplet{int x; int y; int gcd;};
//Solving ax + by = gcd(a,b)
Triplet extentedEuclid(int a, int b){
Triplet ans;
if(b == 0){
ans.x = 1;
ans.y = 0; // technically, can be anything. ax + by = gcd(a,0), here b==0
ans.gcd = a;
return ans;
}
Triplet subAns = extentedEuclid(b,a%b);
ans.x = subAns.y;
ans.y = subAns.x - (a/b)*subAns.y;
ans.gcd = subAns.gcd;
return ans;
}
or can also be written like:-
// Solving ax + by = gcd(a,b)
int extentedEuclid(int a, int b, int& x, int& y){
if(b == 0){
x = 1;
y = 0;
return a;
}
int x1, y1;
int g = extentedEuclid(b, a%b, x1, y1);
x = y1;
y = x1 - (a / b) * y1;
return g;
}
Diophantine Equations:
- Equations that are polynomial in nature and there solutions are always integral values.
- Linear Diophantine Equations
- Form: Ax + By = C ; where A,B,C are all integers. ----- (1)
- Equation of degree one
- Solutions(value of x and y) are integers.
- Assuming x and y are integers, then,
- => Ax is integer, By is integer and we know gcd(A,B) divides Ax, By.
- => gcd(A,B) divided (Ax + By) as well.
- => gcd(A,B) divided (C) as well. -----(2)
- => If (2) is not true, no integral solutions exist for above equation.
- solution of theses equation (1) are
x = x' + (b/d)*t and y = y' - (a/d)*t
MMI - Modulo Multiplicative Inverse
Multiplicative Inverse of x is y, if xy = 1.
Modulo Multiplicative Inverse of x is y w.r.t m,
- if xy ≅ 1 (mod m) (
≅means congruent.) - if xy(modm) ≅ 1 (
≅means congruent.) - or xy is congruent to 1 mod m.
- or (xy)mod m = 1 modm
- if xy ≅ 1 (mod m) (
Naive Approach O(m):
- To find the y. we can put y from (0 to m-1) in xy mod m and check which one is giving 1.That will the MMI of x wrt m.
- Ex- 2 is MMI of 3 wrt 5.
Note: For every value, MMI may not Exist. Just like inverse(0) does not exist.
If gcd(x, m) = 1, then only MMI of x exist wrt m.(A & m should be co-prime) or we can say if one of them is prime.
- Proof:-
- xy modm = 1 modm
- (xy - 1) modm = 0
- => xy - 1 = m*q (q will be an integer.)
- => xy - mq = 1
- => xy + mQ = 1 ;(where Q = -q)
- => y will exist and a integer, if
gcd(x,m) divides 1----(1) - => only one value satisfies (1) , i.e. gcd(x,m) = 1.
- => if MMI(x,m) is to be a integer value y, then gcd(x,m) has to be 1.
- Proof:-
Extended Euclidean Algorthim Approach to find MMI: Optimized O(log(min(A,M)))
- We want to find out MMI of A wrt to M then:-
- => Ax + My = gcd(A,M) = 1(so that MMI exist); taking mod on both side
- => (Ax + My) mod M = 1 mod M
- => Ax mod M + My mod M = 1 mod M
- => Ax mod M + 0 = 1 mod M
- => Ax mod M = 1 mod M => x is the MMI of A as Ax = 1 mod M
- We can find that x using Extended Euclidean Algo(EEA).
- Conclusion: To find MMI of A wrt M.
- Check gcd(A,M) = 1
- & Find x in Ax + My = 1 using EEA
- x = y' & y = x' - (A/M) * y'
- Once we get the MMI we can put it into (a / b) % m = (a % m * MMI(b,m)) % m and get the answer.
- Note: If MMI is coming -ve add m to it.
- Note: If gcd(A,m) != 1 => inverse doesn't exist.
- MMI(b,m) = x = y' = (y'+m) % m.
int MMI(a,m){
Triplet ans = extendedEuclid(a,m);
return ans.x;
}Fermet's Little Theorem
- a^p ≅ a mod p -------------------- (0)
- To find MMI(a,m). If m is prime p.
- then
p always divides a^p - a. ------- (1) - also
a^(p-2) mod p is your MMI(a,p). - How ?
- we want a*X = 1 mod p right? ------ (2)
- and we know a^p - a ≅ 0 mod p (via 1)
- => a*(a^(p-1) - 1) ≅ 0 mod p
- since a and p are coprime. p must be dividing (a^(p-1) - 1).
- => (a^(p-1) - 1) ≅ 0 mod p
- adding 1 on both side
- => a^(p-1) ≅ 1 mod p
- => a*(a^(p-1)) mod p = 1 mod p ---- (3)
- Comparing (2) and (3)
MMI(a,p) = X = a^(p-2) mod p.- or simply divide (0) by a^2. we get inverse(a) modp = a^p-2. given p is prime.
- To calculate this term we need to learn Modular Exponentiation.
- let say i want to calulate 2/3 mod 1e9+7
- since m is prime. ans = 2*(3^(1e9 + 7 - 2)mod 1e9+7)
Euler Totient Function Φ(n)
- Φ(n) means number of numbers <= n, which are coprime to n,
- means all those i's, 1<= i <=n, such that gcd(i,n) = 1.
- Φ(3) = 2 (values are: 1,2)
- Φ(4) = 2 (values are: 1,3)
- Φ(5) = 4 (values are: 1,2,3,4)
- Φ(n) = n(1-1/p1)(1-1/p2)*....., where pi are the prime factors of n.
- Proof is simple, no need to learn, google if needed in future.
- If need to calculate phi of all the numbers from 1 to n. use approach like did in sieve to multiply multiples of prime by (1-1/pi). Complexity is same (NloglogN).
// Φ(i) = i*(1-1/p1)*(1-1/p2)*....., where pi are the prime factors of i.
void eulerPhiTillN(int n){
vector<int> phi(n+1,0);
for(int i=0;i<=n;i++){
phi[i] = i; // saving n part of formula in Φ(n)
}
phi[0] = 0;
phi[1] = 1;
for(int i=0;i*i<=n;i++){
if(phi[i]==i){ // if number is prime
phi[i] = i-1; // Φ(prime number) = p-1 (values are: 1,2,3,4,..........p-1)
for(int j=2*i; j<=n; j+=i){ // here j will start from 2*i, not from i*i, as 10 will also need to be multiplied by(1-1/5)
// phi[j] *= (1-1/i); // as 1/i will always be 0, multiply after taking lcm
phi[i] *= (i-1);
phi[i] /= i;
}
}
}
for(int i=0;i*i<=n;i++){
cout<<phi[i]<<" ";
}
cout<<endl;
}
int main(){
int n; cin>>n;
eulerPhiTillN(n);
}- Φ(n) means number of numbers <= n, which are coprime to n,
Handling Values larger than long long via mod
- Represent value as string
- now how to take mod of string number?
- start from left and do result = (result*10 + (int)(str[i]-'0'))%m, for all i's.
string num = "2141904793704971047934701374"
int mod = 101;
int result = 0;
for(int i = 0; str[i]!='\0'; i++){
result = (result*10 + (int)(str[i]-'0')) % m;
}
cout<<result<<endl;
- or use Python 😁
5.2 Prefix and Partial Sums
Prefix Sums
[for range Queries, no updation between queries]:- Precalculating the prefixes of array is prefix Sums in which operators allows removing contribution(+,^ and more).
- Conclusion. Via prefix sum we can find Σi (Ai), where i goes from l to r in O(1). via precalculation of prefix sums. where Ai can be Ai, iA[i], (2^i)A[i] or some other expression.
Partial sums
[for range updation, and no queries in between]:- Let we have to add(update) X to every number in a range [L,R] of an array.
- we do add +X to arr[L] and -X to arr[R+1] for every query
- then we create a prefix sum array which would be the final answer.
- This is called partial sums as we are storing partial sums on index L and R+1 part of array. and later we are gonna use them.
For both range queries and updation, we use Segment/Fenwick Tree.
5.3 Greedy Technique
Exchange Arguments- Greedy algorithms generally take the following form. Select a candidate greedily according to some heuristic, and add it to your current solution if doing so doesn’t corrupt feasibility. Repeat if not finished. ”Greedy Exchange” is one of the techniques used in proving the correctness of greedy algorithms. The idea of a greedy exchange proof is to incrementally modify a solution produced by any other algorithm into the solution produced by your greedy algorithm in a way that doesn’t worsen the solution’s quality. Thus the quality of your solution is at least as great as that of any other solution. In particular, it is at least as great as an optimal solution, and thus, your algorithm does in fact return an optimal solution.
- Main Steps
- After describing your algorithm, the 3 main steps for a greedy exchange argument proof are as follows:
- Step 1: Label your algorithm’s solution, and a general solution. For example, let A = {a1, a2,...,ak} be the solution generated by your algorithm, and let O = {o1, o2,...,om} be an arbitrary (or optimal) feasible solution.
- Step 2: Compare greedy with other solution. Assume that your arbitrary/optimal solution is not the same as your greedy solution (since otherwise, you are done). Typically, you can isolate a simple example of this difference, such as one of the following: • there is an element of O that is not in A and an element of A that is not in O, or • there are 2 consecutive elements in O in a different order than they are in A (i.e. there is an inversion).
- Step 3: Exchange. Swap the elements in question in O (either swap one element out and another in for the first case, or swap the order of the elements in the second case), and argue that you have a solution that is no worse than before. Then argue that if you continue swapping, you can eliminate all differences between O and A in a polynomial number of steps without worsening the quality of the solution. Thus, the greedy solution produced is just as good as any optimal (or arbitrary) solution, and hence is optimal itself.
- Comments
- • Be careful about using proofs by contradiction starting with the assumption G 6= O. Just because your greedy solution is not equal to the selected optimal solution does not mean that greedy is not optimal – there could be many optimal solutions, and your greedy one just isn’t the optimal solution you selected. So assuming G 6= O may not get you any contradiction at all, even if greedy works.
- • You need to argue why the 2 elements you’re swapping even exist out of order, or exist in O but not in A, etc.
- • Remember you need to argue that multiple swaps can get you from your selected solution to greedy, as one single swap will usually not suffice. Also, make sure that any step you make (and not just the first one) doesn’t hurt the solution quality.
- Example: Minimum Spanning Tree
- We are given a graph G = (V,E), with costs on the edges, and we want to find a spanning tree of minimum cost. We use Kruskal’s algorithm, which sorts the edges in order of increasing cost, and tries to add them in that order, leaving edges out only if they create a cycle with the previously selected edges.
- Proof of Correctness for Kruskal’s Algorithm: Let T = (V,F) be the spanning tree produced by Kruskal’s algorithm, and let T∗ = (V,F∗) be a minimum spanning tree. If T is not optimal then F∗ 6= F, and there is an edge e ∈ F∗ such that e /∈ F. Then e creates a cycle C in the graph T + e, and at least one edge f of this cycle crosses the cut defined by T∗ − e. Furthermore, the reason e is not in F must be that when the algorithm considered adding e, the rest of C was already in the tree. Since we consider edges in increasing order of cost, this means that e must be the most expensive edge in C, and so cost(f) ≤ cost(e). If we add the edge f to the graph T∗ − {e}, then we reconnect the graph and create a spanning tree.
- Also, cost(T∗ − {e}∪{f}) = cost(T∗) −cost(e) +cost(f) ≤ cost(T∗), and so we have created a new spanning tree of no more cost than T∗, but with one more edge in common with T. We can do this for every edge that differs between T and T∗. The two trees differ on at most all n − 1 edges, so after n − 1 steps we obtain the tree T of no more cost than T∗. This contradicts the assumption that T was not optimal.
5.4 Binary Search
Binary Search only works on sorted arrays.(Monotonic Functions)
Binary Search does not work on sorted linked lists because getting the middle element will take O(n) in itself..
Valid Monotonic Function F(x) values.
- YYYYYYYYYNNNNNNN
- NNNNNNNNYYYYYYYY
- YYYYYYYYYYYYYYYY
- NNNNNNNNNNNNNNNN
try to map question to
check(x)function that returns Y or N, which maps question's answer to a monotonic function F(x).then move low and high pointers accordingly, save answer according to what you wanna find out, first/last
Yor first/lastN.initial ans value = (the case in which, we will not update
ansvariable, inside while loop).
// for finding the idx of sorted rotated array.
vector<int> nums = {5, 6, 1, 2, 3, 4};
// Note: this function doesn't give monotonic search space, if array contains duplicate values like [5,5,5,5,4,4,5]
bool check(int idx) {
int n = nums.size();
return nums[idx] > nums[n - 1];
// space generated here will be YYYYYNNNNN, and we need to find first N.
}
int solve() {
int n = nums.size();
int low = 0;
int high = n - 1;
int ans = 0; // 0 because my ans will not change for the case my check function always returns true,
// i.e. YYYYYYYYY => in that case my array is sorted => answer will be 0, no rotation.
while (low <= high) {
int mid = (low + high) / 2;
if (check(mid)) {
low = mid + 1;
} else {
ans = mid;
high = mid - 1;
}
}
cout << ans << endl;
}
- *We can also pass our check function to STL lower_bound and upper_bound function to work according to us.
- Note: floor(a/b) = a/b (integer divison)
- Note: ceil(a/b) = (a +(b-1))/b (integer divison)
- Standard types of Binary Search (Thanks to Algozenith)
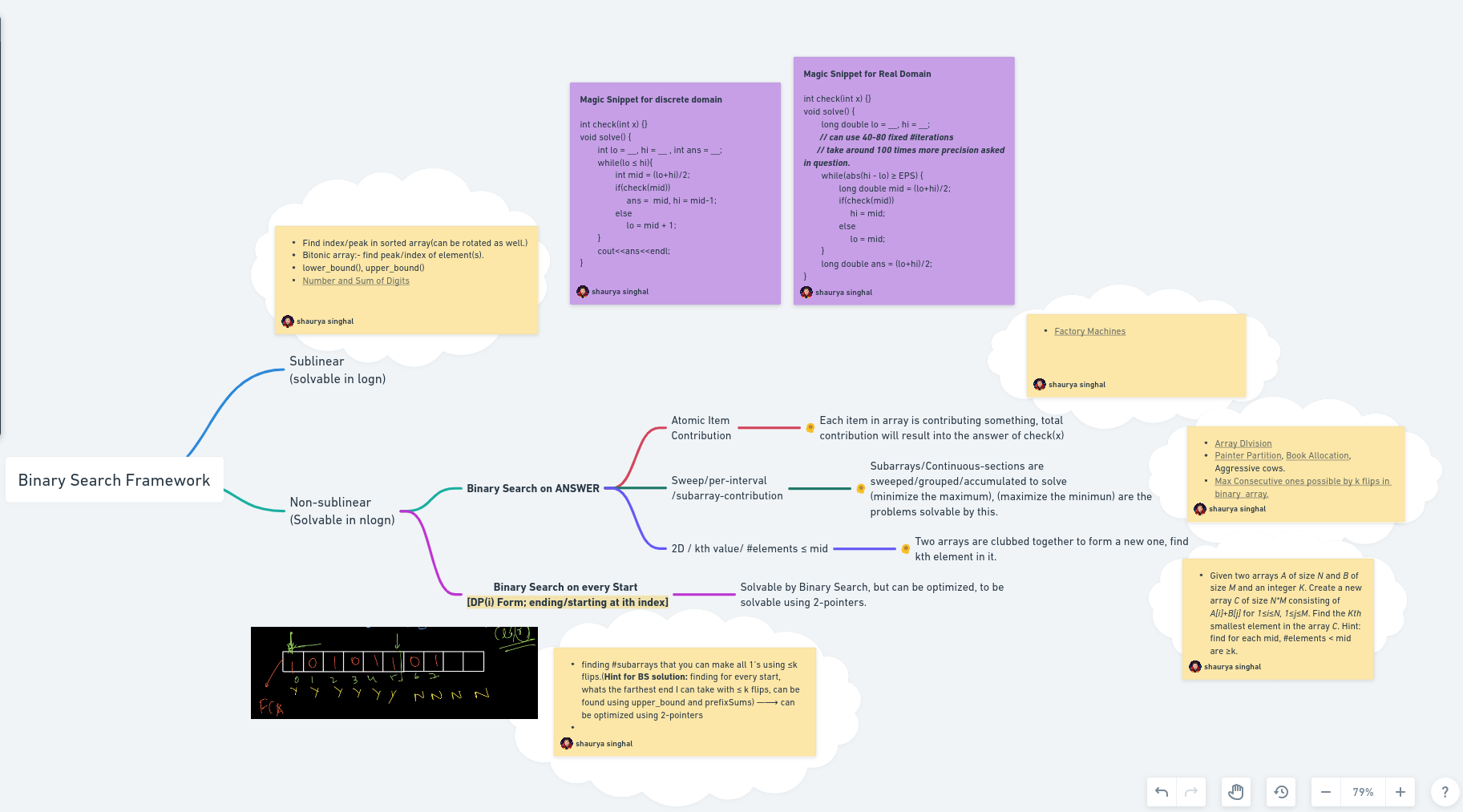
- Binary search on every Start problems are optimized using two-pointer technique.
5.4.3 Ternary Search
- Searching for maxima/minima of a parabolic function (bell shaped curve). i.e strictly increasing then strictly decreasing and vice-versa.
// for increasing then decresing func.
int f(x) { return -x*x + 3*x + 4; }
void solve(){
long double lo = 0; long double hi = n;
while(hi - lo > eps){
long double mid1 = lo + (hi-lo)/3;
long double mid2 = lo + 2 * (hi-lo) / 3;
if(f(mid1) < f(mid2)) lo = mid1;
else hi = mid2;
}
cout << lo << f(lo) << endl;
}
- We can solve the same problem using binary Search by considering mid2 to be mid1 + eps.
// for increasing then decresing func.
int f(x) { return -x*x + 3*x + 4; }
void solve(){
long double lo = 0; long double hi = n;
while(hi - lo > eps){
long double mid1 = lo + (hi-lo)/3;
long double mid2 = mid1 + eps;
if(f(mid1) < f(mid2)) lo = mid1;
else hi = mid2;
}
cout << lo << f(lo) << endl;
}
// Hence use this only, as no new method need to learned, BYE BYE Ternary Search :)
5.5. Two Pointers
- Two pointers === variable size sliding window. -> Good Segment Technique.
- Sliding Window === fixed size sliding window.
- For all positive number array:-
- Finding length of longest sub-array, with sum ≤ k.
- Finding length of smallest sub-array, with sum ≥ k.
- Finding no. of subarrays with sum ≤ k.
- Finding no. of subarrays with sum ≥ k.
- Tip: They generally follows Good Segment Technique.
Good Segment: is a segment that satisfies what we want(sum ≤ k). It follow either of the property:- Increasing Good Segement: If a sub-array is good segment, then all subarrays containing this sub-array is also good. (in sum ≥ k question.)
- Decreasing Good Segement: or If a sub-array is good segment, then all subarrays inside this sub-array is also good. (in sum ≤ k question.)
- Increasing Good Segment question can always be seen/converted into Descreasing Good segment. Hence one code works everytime.😎
// Template for 2-pointes, good Segment: decreasing.
// [l, r], both are inclusive
int r = -1, l = 0; // initially no answer.
int ans = 0;
//Q:- no.of flips not more than k :-> get longest 1's subarray
// some datastructure to keep
int zeros_count = 0;
while(l<n){
while(r + 1 < n && /* datastructure check before insertion */zeros_count + (1 - arr[r + 1]) <= k) {
zeros_count += (1 - arr[r + 1]); // datastructure insertion
r++;
}
ans = max(ans, r - l + 1);
if(r < l){
// when we have zero element in window
l++;
r = l - 1;
} else {
zeros_count -= (1 - arr[l]); // datastructure removal
l++;
}
}
cout<<ans<<endl;
```
// Template for 2-pointes, good Segment: increasing(above oppsite thinking) -> just one line addition.
// [l, r], both are inclusive
int r = -1, l = 0; // initially no answer.
int ans = 0;
//Q:- no.of flips >=k :-> get longest 1's subarray
// some datastructure to keep
while(l<n){
while(r + 1 < n && /* datastructure check before insertion */ /* note: go_till_invalid() */) {
// datastructure insertion here
r++;
}
if(r + 1 < n) {
ans = max(ans, r - l + 1);
}
if(r < l){
// when we have zero element in window
l++;
r = l - 1;
} else {
// datastructure removal
l++;
}
}
cout<<ans<<endl;
```
### 5.6 Bit Manipulation
- `__builtin_popcount()` = count #set bits.
- `__builtin_popcountll()` = count #set bits for long long.
- `__builtin_clz()` = count leading zeros.
- `__builtin_ctz()` = count trailing zeros.
- All are provided by compiler.
- get ith bit of a number n, two ways:
- `(n >> i) & 1` => use this one.
- `n & (1 << i)` => if i > 32, then `1 << i` will not give correct result, use `1LL << i` instead if want to use this expression only.
- **~x = -(x + 1)**
- ~7 = -8
- ~17 = -18
- ~(-7) = 6
- all 1's is -1. i.e. 0b111111...32times = -1
- Printing all subsets of array using bitmask
- XOR of first N Natural Numbers follow a pattern:
- 1 = 1 ---> always 1
- 1^2 = 3 -----> N + 1
- ..^3 = 0 ------> always 0
- ..^4 = 4 -----> N
- ..^5 = 1 ------> always 1
- ..^6 = 7 -----> N + 1
- ..^7 = 0 -----> always 0
- ..^8 = 8 -----> N
- and so on...
- Just like Prefix Sum , we find out Sum(l,r) = PreSum[r] - PreSum[l-1]
- We have Prefix Xor , we find out XOR(l,r) = PreXor[r] ^ PreXor[l-1]
- a + b = a & b + a | b
- a + b = 2\*(a & b) + a ^ b
```cpp
// n can atmax be of 64.
int arr[] = {1, 2, 3};
int n = 3;
for(int mask = 0; mask < (1LL << n); mask++){
for(int j = 0; j < n; j++){
if((mask >> j) & 1){
cout << arr[j] << " ";
}
}
cout << endl;
}
```
- Types of Problems:
- **Bit in-dependent**: result of xth bits of numbers will not depend on other yth bits. Hence can solve for each bit seperately.
- Ex: Doing XOR, AND, OR of numbers is bit-independent.
- **Bit dependent**: result of xth bits of numbers will be depending on other yth bits.
- Ex: Doing +, \*, -, / of numbers is bit-dependent.
### 5.7 Linked List
- The Diff-Pointer Technique (Finding Difference in length of LLs using pointers)
- eg: Find intersection node of LL.
- The Slow-and-Fast-pointer Technique
- eg: Find middle node of LL.
### 5.8 Trie
- A trie (pronounced as "try") or prefix tree is a tree data structure used to efficiently store and retrieve keys in a dataset of strings.
- Use for fast re`trie`val of data or Autocompletion of words.
- can use hashtable instead of trie to store all words with prefixes as key
```
- words = {"bad" , "ban" , ......}
- let each word is atmost m words(let say 20) long and we have n words.
hashtable:-
key | values
b | [bad,ban]
ba | [bad,ban]
bad | [bad]
ban | [ban]
space complexity Ω(m*n)
Insertion = Deletion = O(m) // inserting for each prefixes
Searching/retrieval = O(1) for any prefix.
```
- But we use trie (26-ary tree) because common prefixes are inserted into trie only once, saving a lot of space
- Space complexity is much less than O(m\*n)
- Searching/iseriton/deletion = O(m) = O(length of word) = O(20) = constant.
- spacing is better, rest is almost constant => we use tries instead.
### 5.9 Interative Problems
- Remove fastIO and use endl instead of '\n'.
- We can write query() function that take cares of input.
```cpp
int query(){
}
```
### 5.10 PBDS
- A Datastructure which is like set, but with additional functionlity
- We can access kth element in this set using find_by_order.
- Keeps elements sorted just like set.
- access the kth element in set is O(n)
- access the kth element in Pbds is O(logn).
```cpp
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
using namespace __gnu_pbds;
typedef tree<int, null_type, less<int>, rb_tree_tag, tree_order_statistics_node_update> pbds;
// int ----> datatype of item in pbds set
// pair<int, int> -----> can be used to make this set, a multiset. where second value is unique across.
// typedef tree< pair<int,int>, null_type, less<pair<int,int>>, rb_tree_tag, tree_order_statistics_node_update> pbds;
```
#### Functions in pbds:- O(logN)
- void pbds.insert(ele)
- iterator pbds.find_by_order(int idx) <!-- Finds kth indexed element and returns its iterator, i.e returns an iterator to the k-th largest element (counting from zero). -->
- int pbds.order_by_key(int key) <!-- returns index of a key if present, if not returns >= th element index, i.e. the second — the number of items in a set that are strictly smaller than our item -->
- iterator pbds.erase(it)
- iterator pbds.lower_bound(int key)
- iterator pbds.upper_bound(int key)
#### Fibonacci Number
- Binet's Formula, Works for small fib numbers. Formula = (phi^n - (phiCap)^(n)) / sqrt(5), where phi = (1+sqrt(5)/2), phiCap = (1-sqrt(5)/2), Phi is also called Golden Ratio
- [Codeforces Hack](https://codeforces.com/blog/entry/14516/) - O(logn \* loglogn)
- If n is even, f(n) = f(n/2)_f(n/2) - f(n/2-1)_ f(n/2-1) ;i.e. half<sup>2</sup> - (half-1)<sup>2</sup>
- If n is odd, f(n) = f(n/2)_f(n/2+1) - f(n/2)_ f(n/2-1) ;i.e. half*(half+1) - half*(half-1)
- Via Matrix Exponentiation: Time: O(logn).
- Properties of Fibonacci Numbers
1. **Sum of first N fibonacci number** = (n+2)th Fibonacci - 1
- F0 + F1 + F2 + ... + Fn = F(n+2) - 1
2. **Sum of square of first N fibonacci Numbers** is Product of F(n)\*F(n+1)
- (F0)<sup>2</sup> + (F1)<sup>2</sup> + (F2)<sup>2</sup> + ... + (Fn)<sup>2</sup> + = Fn\*F(n+1)
3. GCD of two fibonacci numbers(nth and mth) is the gcd(n,m)th Fibonacci number
- gcd(Fn,Fm) = F(gcd(n,m))
### Facts
### 5.11 Others
- Segment Trees
- Fenwick Tree
- Tries
- Computational Geometry
- vectors
- dot product
- cross product
- convex hull
- String Algorithms
- Naive
- KMP
- Binary Lifting